Ordered Bell number

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of $n$ elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.

The 13 possible strict weak orderings on a set of three elements {a, b, c}

The ordered Bell numbers were studied in the 19th century by Arthur Cayley and William Allen Whitworth. They are named after Eric Temple Bell, who wrote about the Bell numbers, which count the partitions of a set; the ordered Bell numbers count partitions that have been equipped with a linear order. Their alternative name, the Fubini numbers, comes from a connection to Guido Fubini and Fubini's theorem on equivalent forms of multiple integrals.

These numbers may be computed via a summation formula involving binomial coefficients, or by using a recurrence relation. Along with the weak orderings, they count several other types of combinatorial objects that have a bijective correspondence to the weak orderings, such as the ordered multiplicative partitions of a squarefree number or the faces of all dimensions of a permutohedron.

Definitions and examples

Weak orderings arrange their elements into a sequence allowing ties. This possibility describes various real-world scenarios, including certain sporting contests such as horse races. A weak ordering can be formalized axiomatically by a partially ordered set for which incomparability is an equivalence relation. The equivalence classes of this relation partition the elements of the ordering into subsets of mutually tied elements, and these equivalence classes can then be linearly ordered by the weak ordering. Thus, a weak ordering can be described as an ordered partition, a partition of its elements, together with a linear order on the sets of the partition. For instance, the ordered partition {a,b},{c},{d,e,f} describes an ordered partition on six elements in which a and b are tied and both less than the other four elements, and c is less than d, e, and f, which are all tied with each other.

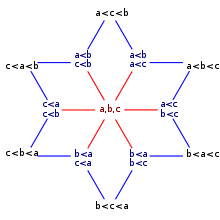
The $n$th ordered Bell number, denoted here $a(n)$, gives the number of distinct weak orderings on $n$ elements. For instance, there are three weak orderings on the two elements a and b: they can be ordered with a before b, with b before a, or with both tied. The figure shows the 13 weak orderings on three elements.

Starting from $n=0$, the ordered Bell numbers $a(n)$ are

1, 1, 3, 13, 75, 541, 4683, 47293, 545835, 7087261, 102247563, ... (sequence A000670 in the OEIS).

History

13 plane trees with ordered leaves and equal-length root-leaf paths, with the gaps between adjacent leaves labeled by the height above the leaves of the nearest common ancestor. These labels induce a weak ordering on the gaps, showing that the trees of this type are counted by the ordered Bell numbers.

The ordered Bell numbers appear in the work of Cayley (1859), who used them to count certain plane trees with $n+1$ totally ordered leaves. In the trees considered by Cayley, each root-to-leaf path has the same length, and the number of nodes at distance $i$ from the root must be strictly smaller than the number of nodes at distance $i+1$, until reaching the leaves. In such a tree, there are $n$ pairs of adjacent leaves, that may be weakly ordered by the height of their lowest common ancestor; this weak ordering determines the tree. Mor & Fraenkel (1984) call the trees of this type "Cayley trees", and they call the sequences that may be used to label their gaps (sequences of $n$ positive integers that include at least one copy of each positive integer between one and the maximum value in the sequence) "Cayley permutations".

Pippenger (2010) traces the problem of counting weak orderings, which has the same sequence as its solution, to the work of Whitworth (1886). These numbers were called Fubini numbers by Louis Comtet, because they count the number of different ways to rearrange the ordering of sums or integrals in Fubini's theorem, which in turn is named after Guido Fubini. The Bell numbers, named after Eric Temple Bell, count the number of partitions of a set, and the weak orderings that are counted by the ordered Bell numbers may be interpreted as a partition together with a total order on the sets in the partition.

The equivalence between counting Cayley trees and counting weak orderings was observed in 1970 by Donald Knuth, using an early form of the On-Line Encyclopedia of Integer Sequences (OEIS). This became one of the first successful uses of the OEIS to discover equivalences between different counting problems.

Formulas

Summation

The $n$th ordered Bell number may be given by a summation formula involving the Stirling numbers of the second kind $\{{\scriptstyle {n \atop k}}\}$, which count the number of partitions of an $n$-element set into $k$ nonempty subsets. A weak ordering may be described as a permutation of the subsets in this partition, and so the ordered Bell numbers (the number of weak orderings) may be calculated by summing these numbers, multiplied by a factorial, $k!$, that counts the number of these permutations:

$$a(n)=\sum _{k=0}^{n}k!\left\{{\begin{matrix}n\\k\end{matrix}}\right\}$$

An alternative interpretation of the terms of this sum is that they count the features of each dimension in a permutohedron of dimension $n$, with the $k$th term counting the features of dimension $n-k$. For instance, the three-dimensional permutohedron, the truncated octahedron, has one volume ($k=0$), 14 two-dimensional faces ($k=1$), 36 edges ($k=2$), and 24 vertices ($k=3$). The total number of these faces is 1 + 14 + 36 + 24 = 75, an ordered Bell number, corresponding to the summation formula above for $n=3$. By general results on summations involving Stirling numbers, it follows that the ordered Bell numbers are log-convex, meaning that they obey the inequality $a(n-1)a(n+1)\geq a(n)^{2}$ for all $n>0$.

By expanding each Stirling number in this formula into a sum of binomial coefficients, the formula for the ordered Bell numbers may be expanded out into a double summation. The ordered Bell numbers may also be given by an infinite series:

$$a(n)=\sum _{k=0}^{n}\sum _{j=0}^{k}(-1)^{k-j}{\binom {k}{j}}j^{n}={\frac {1}{2}}\sum _{m=0}^{\infty }{\frac {m^{n}}{2^{m}}}.$$

Another summation formula expresses the ordered Bell numbers in terms of the Eulerian numbers $\langle {\scriptstyle {n \atop k}}\rangle$, which count the number of permutations of $n$ items in which $k$ items are less than the next item:

$$a(n)=\sum _{k=0}^{n-1}2^{k}\left\langle {\begin{matrix}n\\k\end{matrix}}\right\rangle =A_{n}(2),$$

where $A_{n}$ is the $n$th Eulerian polynomial.

Generating function and approximation

As with many other integer sequences, reinterpreting the sequence as the coefficients of a power series and working with the function that results from summing this series can provide useful information about the sequence. For sequences with faster than exponential growth, such as the ordered Bell numbers, the ordinary generating function may not converge, so instead the exponential generating function is used. For the ordered Bell numbers, it is:

$$\sum _{n=0}^{\infty }a(n){\frac {x^{n}}{n!}}={\frac {1}{2-e^{x}}}.$$

Here, the left hand side is just the definition of the exponential generating function and the right hand side is the function obtained from this summation. The form of this function corresponds to the fact that the ordered Bell numbers are the numbers in the first column of the infinite matrix $(2I-P)^{-1}$. Here $I$ is the identity matrix and $P$ is an infinite matrix form of Pascal's triangle. Each row of $P$ starts with the numbers in the same row of Pascal's triangle, and then continues with an infinite repeating sequence of zeros.

Based on a contour integration of this generating function, the ordered Bell numbers can be expressed by the infinite sum

$$a(n)={\frac {n!}{2}}\sum _{k=-\infty }^{\infty }(\log 2+2\pi ik)^{-(n+1)},\qquad n\geq 1.$$

Here, $\log$ stands for the natural logarithm, whose base is $e\approx 2.718$. This leads to an approximation for the ordered Bell numbers, obtained by using only the first term of this sum and discarding the remaining terms:

$$a(n)\sim {\frac {1}{2}}{n!}(\log _{2}e)^{n+1}.$$

Thus, the ordered Bell numbers are larger than the factorials by an exponential factor, whose base $\log _{2}e$ is approximately $1.4427$. Here, as in Stirling's approximation to the factorial, the $\sim$ indicates that the ratio between the ordered Bell numbers and their approximation tends to one in the limit as $n$ grows arbitrarily large. As expressed in little o notation, this ratio is $1\pm o(1)$, and the $o(1)$ error term is exponentially small in $n$.

Recurrence and modular periodicity

As well as the formulae above, the ordered Bell numbers may be calculated by the recurrence relation

$a(n)=\sum _{i=1}^{n}{\binom {n}{i}}a(n-i).$

The intuitive meaning of this formula is that a weak ordering on $n$ items may be broken down into a choice of some nonempty set of $i$ items that go into the first equivalence class of the ordering, together with a smaller weak ordering on the remaining $n-i$ items. As a base case for the recurrence, $a(0)=1$ (there is one weak ordering on zero items). Based on this recurrence, these numbers can be shown to obey certain periodic patterns in modular arithmetic: for sufficiently large $n$,

$a(n+4)\equiv a(n){\pmod {10}},$

$a(n+20)\equiv a(n){\pmod {100}},$

$a(n+100)\equiv a(n){\pmod {1000}},$ and

$a(n+500)\equiv a(n){\pmod {10000}}.$

Several additional modular identities are given by Good (1975) and Poonen (1988).

Additional applications

As has already been mentioned, the ordered Bell numbers count weak orderings, permutohedron faces, Cayley trees, Cayley permutations, ordered multiplicative partitions of squarefree numbers, and equivalent formulae in Fubini's theorem. Weak orderings in turn have many other applications. For instance, in horse racing, photo finishes have eliminated most but not all ties, called in this context dead heats, and the outcome of a race that may contain ties (including all the horses, not just the first three finishers) may be described using a weak ordering. For this reason, the ordered Bell numbers count the possible number of outcomes of a horse race. In contrast, when items are ordered or ranked in a way that does not allow ties (such as occurs with the ordering of cards in a deck of cards, or batting orders among baseball players), the number of orderings for $n$ items is a factorial number $n!$, which is significantly smaller than the corresponding ordered Bell number.

A parking function, in mathematics, is a finite sequence of positive integers with the property that, for every $i$ up to the sequence length, the sequence contains at least $i$ values that are at most $i$. A sequence of this type, of length $n$, describes the following process: a sequence of $n$ cars arrives on a street with $n$ parking spots. Each car has a preferred parking spot, given by its value in the sequence. When a car arrives on the street, it parks in its preferred spot, or, if that is full, in the next available spot. A sequence of preferences forms a parking function if and only if each car can find a parking spot on or after its preferred spot. The number of parking functions of length $n$ is exactly $(n+1)^{n-1}$. For a restricted class of parking functions, in which each car parks either on its preferred spot or on the next spot, the number of parking functions is given by the ordered Bell numbers. Each restricted parking function corresponds to a weak ordering in which the cars that get their preferred spot are ordered by these spots, and each remaining car is tied with the car in its preferred spot. The permutations, counted by the factorials, are parking functions for which each car parks on its preferred spot. This application also provides a combinatorial proof for upper and lower bounds on the ordered Bell numbers of a simple form,

$$n!\leq a(n)\leq (n+1)^{n-1}.$$

Kemeny (1956) uses the ordered Bell numbers to describe the "complexity" of an n-ary relation, by which he means the number of other relations one can form from it by permuting and repeating its arguments (lowering the arity with every repetition). In this application, for each derived relation, the arguments of the original relation are weakly ordered by the positions of the corresponding arguments of the derived relation.

Velleman & Call (1995) consider combination locks with a numeric keypad, in which several keys may be pressed simultaneously and a combination consists of a sequence of keypresses that includes each key exactly once. As they show, the number of different combinations in such a system is given by the ordered Bell numbers.

Ellison & Klein (2001) point out an application of these numbers to optimality theory in linguistics. In this theory, grammars for natural languages are constructed by ranking certain constraints, and (in a phenomenon called factorial typology) the number of different grammars that can be formed in this way is limited to the number of permutations of the constraints. A paper reviewed by Ellison and Klein suggested an extension of this linguistic model in which ties between constraints are allowed, so that the ranking of constraints becomes a weak order rather than a total order. As they point out, the much larger magnitude of the ordered Bell numbers, relative to the corresponding factorials, allows this theory to generate a much richer set of grammars.