In topography, prominence (also referred to as autonomous height, relative height, and shoulder drop in US English, and drop or relative height in British English) measures the height of a mountain or hill's summit relative to the lowest contour line encircling it but containing no higher summit within it. It is a measure of the independence of a summit. The key col ("saddle") around the peak is a unique point on this contour line and the parent peak is some higher mountain, selected according to various criteria.
Definitions edit
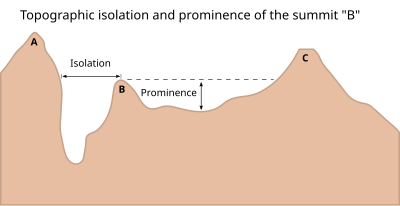
The prominence of a peak is the least drop in height necessary in order to get from the summit to any higher terrain. This can be calculated for a given peak in the following manner: for every path connecting the peak to higher terrain, find the lowest point on the path; the key col (or highest saddle, or linking col, or link) is defined as the highest of these points, along all connecting paths; the prominence is the difference between the elevation of the peak and the elevation of its key col. Mount Everest's prominence is defined by convention as its height, making it consistent with prominence of the highest peaks on other landmasses[citation needed]. An alternative equivalent definition is that the prominence is the height of the peak's summit above the lowest contour line encircling it, but containing no higher summit within it; see Figure 1.
Illustration edit
The parent peak may be either close or far from the subject peak. The summit of Mount Everest is the parent peak of Aconcagua in Argentina at a distance of 17,755 km (11,032 miles), as well as the parent of the South Summit of Mount Everest at a distance of 360 m (1200 feet). The key col may also be close to the subject peak or far from it. The key col for Aconcagua, if sea level is disregarded, is the Bering Strait at a distance of 13,655 km (8,485 miles). The key col for the South Summit of Mount Everest is about 100 m (330 feet) distant.
In mountaineering edit
Prominence is interesting to many mountaineers because it is an objective measurement that is strongly correlated with the subjective significance of a summit. Peaks with low prominence are either subsidiary tops of some higher summit or relatively insignificant independent summits. Peaks with high prominence tend to be the highest points around and are likely to have extraordinary views.
Only summits with a sufficient degree of prominence are regarded as independent mountains. For example, the world's second-highest mountain is K2 (height 8,611 m, prominence 4,017 m). While Mount Everest's South Summit (height 8,749 m, prominence 11 m[1]) is taller than K2, it is not considered an independent mountain because it is a sub-summit of the main summit (which has a height and prominence of 8,848 m).
Many lists of mountains use topographic prominence as a criterion for inclusion in the list, or cutoff. John and Anne Nuttall's The Mountains of England and Wales uses a cutoff of 15 m (about 50 ft), and Alan Dawson's list of Marilyns uses 150 m (about 500 ft). (Dawson's list and the term "Marilyn" are limited to Britain and Ireland). In the contiguous United States, the famous list of "fourteeners" (14,000 foot / 4268 m peaks) uses a cutoff of 300 ft / 91 m (with some exceptions). Also in the U.S., 2000 ft (610 m) of prominence has become an informal threshold that signifies that a peak has major stature. Lists with a high topographic prominence cutoff tend to favor isolated peaks or those that are the highest point of their massif; a low value, such as the Nuttalls', results in a list with many summits that may be viewed by some as insignificant.
While the use of prominence as a cutoff to form a list of peaks ranked by elevation is standard and is the most common use of the concept, it is also possible to use prominence as a mountain measure in itself. This generates lists of peaks ranked by prominence, which are qualitatively different from lists ranked by elevation. Such lists tend to emphasize isolated high peaks, such as range or island high points and stratovolcanoes. One advantage of a prominence-ranked list is that it needs no cutoff since a peak with high prominence is automatically an independent peak.
Parent peak edit
It is common to define a peak's parent as a particular peak in the higher terrain connected to the peak by the key col. If there are many higher peaks there are various ways of defining which one is the parent, not necessarily based on geological or geomorphological factors. The "parent" relationship defines a hierarchy which defines some peaks as subpeaks of others. For example, in Figure 1, the middle peak is a subpeak of the right peak, which is a subpeak of the left peak, which is the highest point on its landmass. In that example, there is no controversy about the hierarchy; in practice, there are different definitions of parent. These different definitions follow.
Encirclement or island parentage edit
Also known as prominence island parentage, this is defined as follows. In Figure 2 the key col of peak A is at the meeting place of two closed contours, one encircling A (and no higher peaks) and the other containing at least one higher peak. The encirclement parent of A is the highest peak that is inside this other contour. In terms of the falling-sea model, the two contours together bound an "island", with two pieces connected by an isthmus at the key col. The encirclement parent is the highest point on this entire island.
For example, the encirclement parent of Mont Blanc, the highest peak in the Alps, is Mount Everest. Mont Blanc's key col is a piece of low ground near Lake Onega in northwestern Russia (at 113 m (371 ft) elevation), on the divide between lands draining into the Baltic and Caspian Seas. This is the meeting place of two 113 m (371 ft) contours, one of them encircling Mont Blanc; the other contour encircles Mount Everest. This example demonstrates that the encirclement parent can be very far away from the peak in question when the key col is low.
This means that, while simple to define, the encirclement parent often does not satisfy the intuitive requirement that the parent peak should be close to the child peak. For example, one common use of the concept of parent is to make clear the location of a peak. If we say that Peak A has Mont Blanc for a parent, we would expect to find Peak A somewhere close to Mont Blanc. This is not always the case for the various concepts of parent, and is least likely to be the case for encirclement parentage.
Figure 3 shows a schematic range of peaks with the color underlying the minor peaks indicating the encirclement parent. In this case the encirclement parent of M is H whereas an intuitive view might be that L was the parent. Indeed, if col "k" were slightly lower, L would be the true encirclement parent.
The encirclement parent is the highest possible parent for a peak; all other definitions indicate a (possibly different) peak on the combined island, a "closer" peak than the encirclement parent (if there is one), which is still "better" than the peak in question. The differences lie in what criteria are used to define "closer" and "better."
Prominence parentage edit
The (prominence) parent peak of peak A can be found by dividing the island or region in question into territories, by tracing the two hydrographic runoffs, one in each direction, downwards from the key col of every peak that is more prominent than peak A. The parent is the peak whose territory peak A is in.
For hills with low prominence in Britain, a definition of "parent Marilyn" is sometimes used to classify low hills ("Marilyn" being a British term for a hill with a prominence of at least 150 m).[2][3] This is found by dividing the region of Britain in question into territories, one for each Marilyn. The parent Marilyn is the Marilyn whose territory the hill's summit is in. If the hill is on an island (in Britain) whose highest point is less than 150 m, it has no parent Marilyn.
Prominence parentage is the only definition used in the British Isles because encirclement parentage breaks down when the key col approaches sea level. Using the encirclement definition, the parent of almost any small hill in a low-lying coastal area would be Ben Nevis, an unhelpful and confusing outcome. Meanwhile, "height" parentage (see below) is not used because there is no obvious choice of cutoff.
This choice of method might at first seem arbitrary, but it provides every hill with a clear and unambiguous parent peak that is taller and more prominent than the hill itself, while also being connected to it (via ridge lines). The parent of a low hill will also usually be nearby; this becomes less likely as the hill's height and prominence increase. Using prominence parentage, one may produce a "hierarchy" of peaks going back to the highest point on the island.[4] One such chain in Britain would read:
Billinge Hill → Winter Hill → Hail Storm Hill → Boulsworth Hill → Kinder Scout → Cross Fell → Helvellyn → Scafell Pike → Snowdon → Ben Nevis.
At each stage in the chain, both height and prominence increase.
Line parentage edit
Line parentage, also called height parentage, is similar to prominence parentage, but it requires a prominence cutoff criterion. The height parent is the closest peak to peak A (along all ridges connected to A) that has a greater height than A, and satisfies some prominence criteria.
The disadvantage of this concept is that it goes against the intuition that a parent peak should always be more significant than its child. However it can be used to build an entire lineage for a peak which contains a great deal of information about the peak's position.
Other criteria edit
To choose among possible parents, instead of choosing the closest possible parent, it is possible to choose the one which requires the least descent along the ridge.
In general, the analysis of parents and lineages is intimately linked to studying the topology of watersheds.
Issues in choice of summit and key col edit
Alteration of the landscape by humans and presence of water features can give rise to issues in the choice of location and height of a summit or col. In Britain, extensive discussion has resulted in a protocol[5] that has been adopted by the main sources of prominence data in Britain and Ireland.[3][6] Other sources of data commonly ignore human-made alterations, but this convention is not universally agreed upon; for example, some authors discount modern structures but allow ancient ones. Another disagreement concerns mountaintop removal, though for high-prominence peaks (and for low-prominence subpeaks with intact summits), the difference in prominence values for the two conventions is typically relatively small.
Examples edit
This section possibly contains synthesis of material which does not verifiably mention or relate to the main topic. (March 2016) |
The key col and parent peak are often close to the subpeak but this is not always the case, especially when the key col is relatively low. It is only with the advent of computer programs and geographical databases that thorough analysis has become possible.
The key col of Denali in Alaska (6,194 m) is a 56 m col near Lake Nicaragua (unless one accepts the Panama Canal as a key col; this is a matter of contention). Denali's encirclement parent is Aconcagua (6,960 m), in Argentina, and its prominence is 6,138 m. To further illustrate the rising-sea model of prominence, if sea level rose 56 m, North and South America would be separate continents and Denali would be 6138 m above sea level. At a slightly lower level, the continents would still be connected, and the high point of the combined landmass would be Aconcagua, the encirclement parent. For the purposes of this article, man made structures such as the Panama Canal are not taken into account. If they were, the key col would be along the 26 m Gaillard Cut and Denali would have a prominence of 6,168 m.
While it is natural for Aconcagua to be the parent of Denali, since Denali is a major peak, consider the following situation: Peak A is a small hill on the coast of Alaska, with elevation 100 m and key col 50 m. Then the encirclement parent of Peak A is also Aconcagua, even though there will be many peaks closer to Peak A which are much higher and more prominent than Peak A (for example, Denali). This illustrates the disadvantage in using the encirclement parent.
Mount Whitney (4421 m) has its key col 1,022 km (635 mi) away in New Mexico at 1347 m on the Continental Divide. Its encirclement parent is Pico de Orizaba (5,636 m), the highest mountain in Mexico. Orizaba's key col is back along the Divide, in British Columbia.
The key col for Mount Mitchell, the highest peak of the Appalachians, is in Chicago, the low point on the divide between the St. Lawrence and Mississippi River watersheds.
A hill in a low-lying area like the Netherlands will often be a direct child of Mount Everest, with its prominence about the same as its height and its key col placed at or near the foot of the hill, well below, for instance, the 113-meter-high key col of Mont Blanc.
Calculations and mathematics edit
When the key col for a peak is close to the peak itself, prominence is easily computed by hand using a topographic map. However, when the key col is far away, or when one wants to calculate the prominence of many peaks at once, software can apply surface network modeling to a digital elevation model to find exact or approximate key cols.[7][8]
Since topographic maps typically show elevation using contour lines, the exact elevation is typically bounded by an upper and lower contour, and not specified exactly. Prominence calculations may use the high contour, giving in a pessimistic estimate,[9][10] the low contour, giving an optimistic estimate, their mean, giving a "midrange" or "rise" prominence,[11] or an interpolated value, customary in Britain.
The choice of method depends largely on the preference of the author and historical precedent. Pessimistic prominence, and sometimes optimistic prominence, were for many years used in US and international lists, but mean prominence is becoming preferred.[12]
Wet prominence and dry prominence edit
There are two varieties of topographic prominence: wet prominence and dry prominence.[13] Wet prominence is the standard topographic prominence discussed in this article. Wet prominence assumes that the surface of the earth includes all permanent water, snow, and ice features. Thus, the wet prominence of the highest summit of an ocean island or landmass is always equal to the summit's elevation.
Dry prominence, on the other hand, ignores water, snow, and ice features and assumes that the surface of the earth is defined by the solid bottom of those features. The dry prominence of a summit is equal to its wet prominence unless the summit is the highest point of a landmass or island, or its key col is covered by snow or ice. If its highest surface col is on water, snow, or ice, the dry prominence of that summit is equal to its wet prominence plus the depth of its highest submerged col.
The dry prominence of Mount Everest is, by convention, equal to its wet prominence (8848 m) plus the depth of the deepest hydrologic feature (the Challenger Deep at 10,911 m), or 19,759 m.[citation needed] The dry prominence of Mauna Kea is equal to its wet prominence (4205 m) plus the depth of its highest submerged col (about 5125 m), or about 9330 m, giving it the world's second greatest dry prominence after Mount Everest.[13] The dry prominence of Aconcagua is equal to its wet prominence (6962 m) plus the depth of the highest submerged col of the Bering Strait (about 50 m), or about 7012 m.
Dry prominence is also useful for measuring submerged seamounts. Seamounts have a dry topographic prominence, a topographic isolation, and a negative topographic elevation.
List of most prominent summits on Earth by 'dry' prominence edit
See also edit
- Height above average terrain (HAAT) – a similar measurement for FM and TV transmitters
- Jut (topography)
- Ultra-prominent summit
- Lists
- List of mountain lists
- List of tallest mountains in the Solar System
- List of the most prominent summits of the world
- List of ultra-prominent summits of Africa
- List of ultra-prominent summits of Antarctica
- List of ultra-prominent summits of Australia
- List of ultra-prominent summits of the Alps
- List of the most prominent summits of the British Isles
- List of European ultra-prominent peaks
- List of ultra-prominent summits of North America
- List of the most prominent summits of Greenland
- List of the most prominent summits of Canada
- List of the most prominent summits of the Rocky Mountains
- List of the most prominent summits of the United States
- List of the most prominent summits of Mexico
- List of the most prominent summits of Central America
- List of the most prominent summits of the Caribbean
- List of ultra-prominent summits of South America
- List of islands by highest point
References edit
- ^ "Mount Everest-South Summit, China/Nepal". Peakbagger.com.
- ^ Dawson, Alan (1997). The Hewitts and Marilyns of England. Glasgow: TACit Press. There are several related booklets covering Britain and Ireland. ISBN 0-9522680-7-8.
- ^ a b "The Database of British and Irish Hills". hills-database.co.uk and hill-bagging.co.uk. Retrieved 2016-04-21.
- ^ "More Relative Hills of Britain" (PDF). Mark Jackson. Retrieved 2016-04-22.
- ^ "Defining the Summits and Cols of Hills" (PDF). The Database of British and Irish Hills. Retrieved 2016-04-21.
- ^ "MountainViews". mountainviews.ie. Retrieved 2016-04-21.
- ^ "WinProm". GitHub. Retrieved 2017-01-13.
- ^ "Topographic prominence". Retrieved 2017-01-13.
- ^ "Help and Glossary". Peakbagger.com. Retrieved 2013-01-31.
- ^ "Accuracy of heights from Ordnance Survey maps" (PDF). The Database of British and Irish Hills. Retrieved 2016-04-22.
- ^ "Definition of Rise". ListsOfJohn.com. Retrieved 2013-01-31.
- ^ "United States P2000 Home Page". peaklist.org. Retrieved 2021-04-17.
- ^ a b Adam Helman, The Finest Peaks–Prominence and Other Mountain Measures, 2005.
- ^ "Flood Map: Elevation Map, Sea Level Rise Map". www.floodmap.net. Retrieved 2021-06-07.